다익스트라(Java)

다익스트라란?

다익스트라 알고리즘은 최단 거리를 구하는 알고리즘입니다.

조건

다익스트라 알고리즘을 사용하여 문제를 풀기 위해서는 조건이 있습니다.

• 음수 가중치가 없어야 한다.

음수 가중치가 있는 그래프에서 최단 거리를 구하기 위해서는 벨만-포드 알고리즘을 사용하면 됩니다.

다익스트라 알고리즘 방식

그렇다면 어떻게 그래프의 최단 거리를 구하는걸까요?

1. 아직 방문하지 않은 정점 중 출발지로부터 가장 가까운 정점을 방문합니다. -> 우선순위 큐
2. 해당 정점을 거쳐 갈 수 있는 정점의 거리가 이전 기록한 값보다 작으면 갱신합니다.

(1)번 과정에서 출발지로부터 가장 가까운 정점을 방문해야 하기 때문에 구현할 때에는 우선순위 큐를 사용합니다. 예시를 통해 알아봅시다.

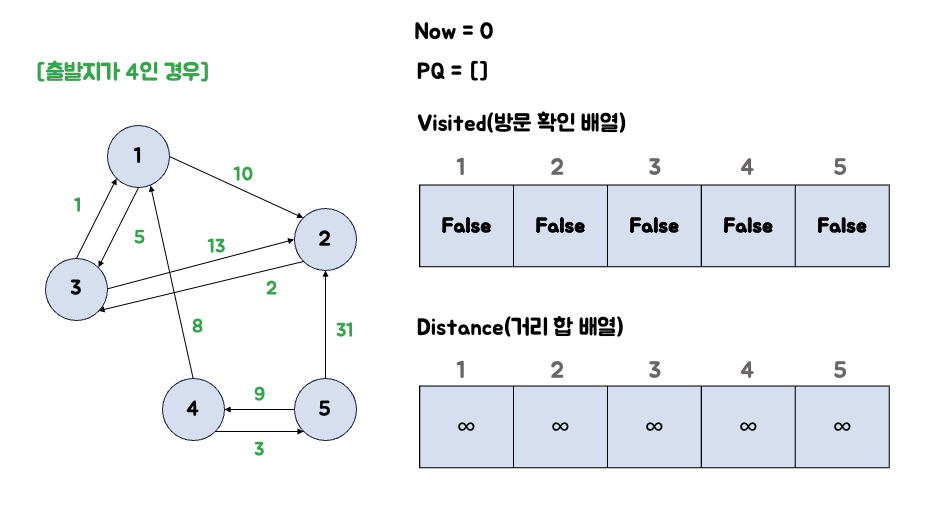
0. 예시 그래프

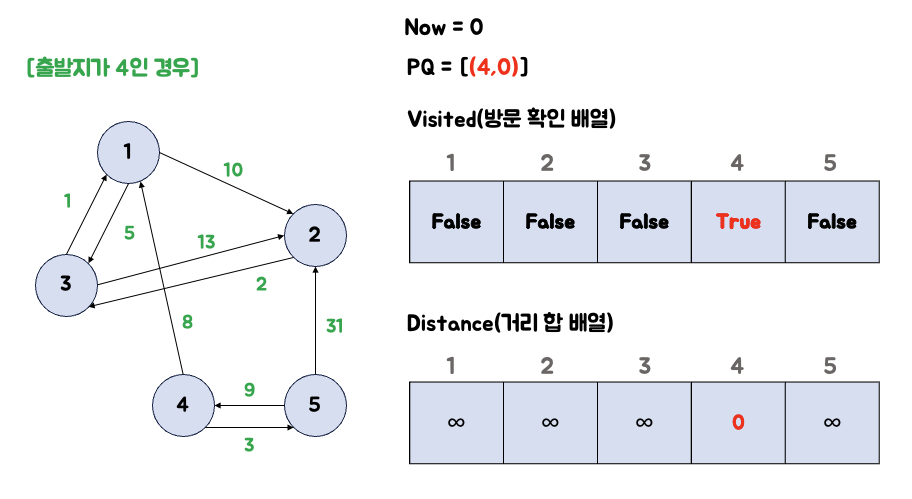
1. 출발지 4를 우선순위 큐에 넣는다.

출발지인 4를 우선순위 큐에 넣고 방문 처리를 합니다.

출발지는 최단 거리가 0이므로 거리 배열도 0으로 갱신해 줍니다.

2. 큐에서 4번 노드를 꺼내서 연결된 노드의 거리를 갱신한다.

큐에서 4를 꺼냅니다. 4번 노드와 연결되어 있는 노드들의 값을 갱신하고, 우선순위 큐에 넣습니다.

• 5번 노드 : 현재 값(무한대)보다 3이 더 작으므로 3으로 갱신합니다.
• 1번 노드 : 현재 값(무한대)보다 8이 더 작으므로 8로 갱신합니다.

위와 같은 동작을 우선순위 큐가 빌 때까지 반복합니다!

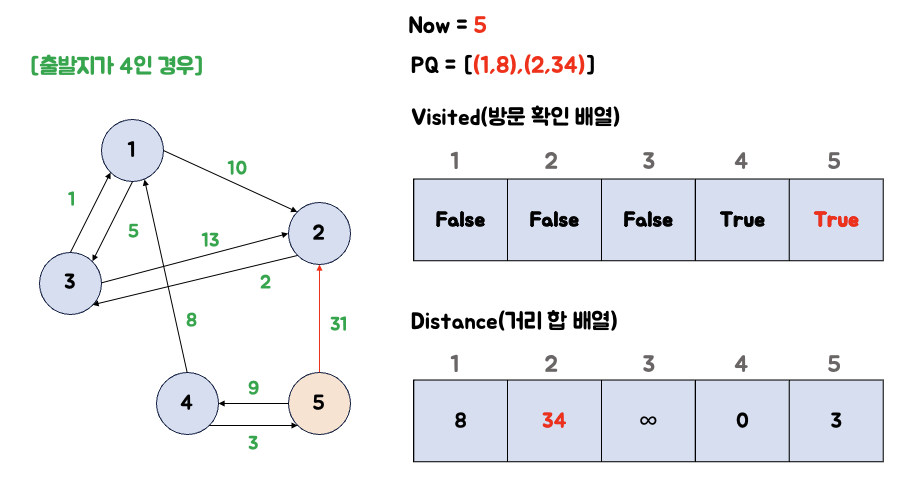
3. 큐에서 5번 노드를 꺼내서 연결된 노드의 거리를 갱신한다.

큐에서 5를 꺼냅니다. 5번 노드와 연결되어 있는 노드들의 값을 갱신하고, 우선순위 큐에 넣습니다.

• 2번 노드 : 현재 값(무한대)보다 (3+31)이 더 작으므로 34로 갱신합니다.

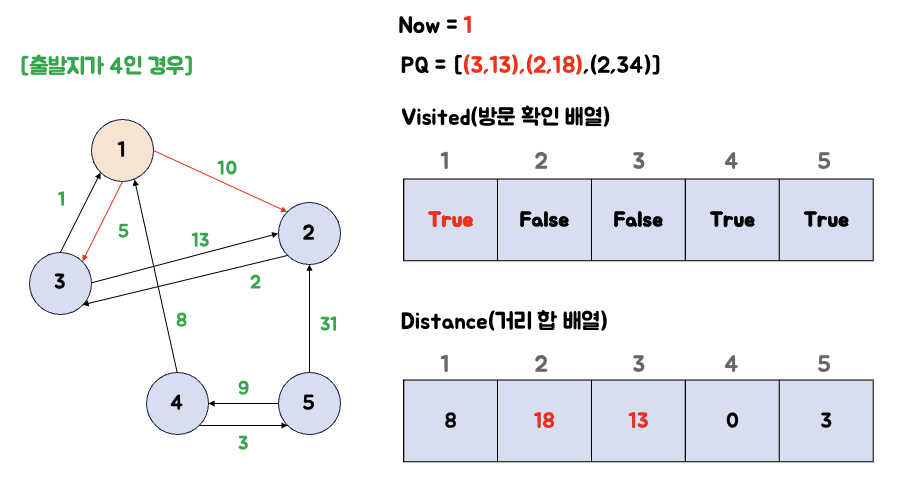
4. 큐에서 1번 노드를 꺼내서 연결된 노드의 거리를 갱신한다.

큐에서 1를 꺼냅니다. 1번 노드와 연결되어 있는 노드들의 값을 갱신하고, 우선순위 큐에 넣습니다.

• 2번 노드 : 현재 값(34)보다 (8+10)이 더 작으므로 18로 갱신합니다.
• 3번 노드 : 현재 값(무한대)보다 (8+5)가 더 작으므로 13로 갱신합니다.

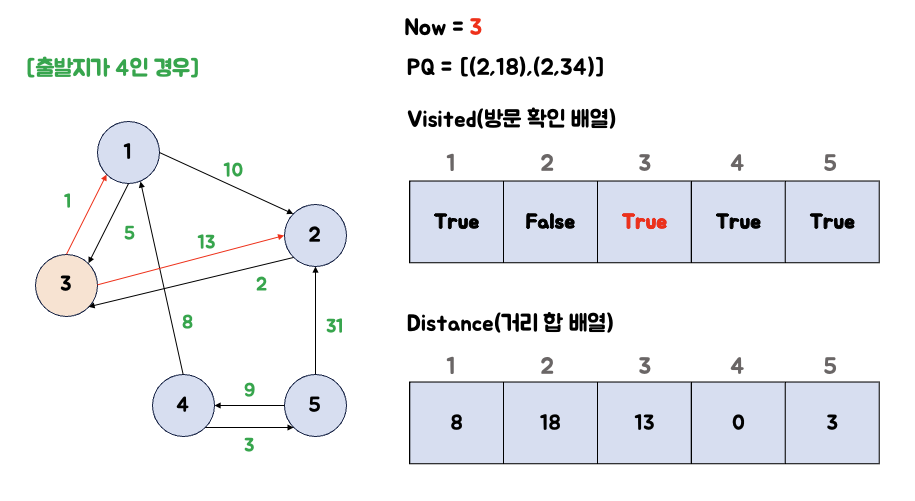
5. 큐에서 3번 노드를 꺼내서 연결된 노드의 거리를 갱신한다.

큐에서 3을 꺼냅니다. 3번 노드와 연결되어 있는 노드들의 값들을 갱신하지 않았으므로, 우선순위 큐에 넣지 않습니다.

• 1번 노드 : 현재 값(8)이 (8+5+1)보다 더 작으므로 갱신하지 않습니다.
• 2번 노드 : 현재 값(18)이 (8+5+13)보다 더 작으므로 갱신하지 않습니다

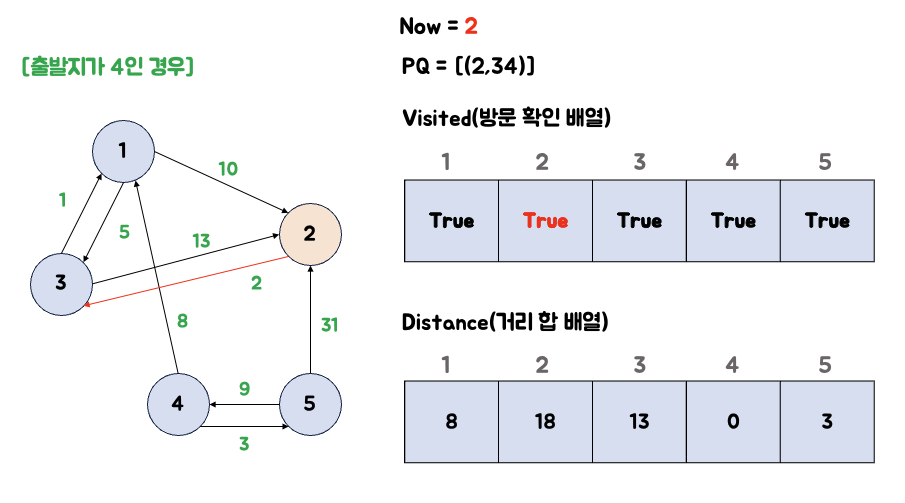
6. 큐에서 2번 노드를 꺼내서 연결된 노드의 거리를 갱신한다.

큐에서 2를 꺼냅니다. 2번 노드와 연결되어 있는 노드의 값은 갱신하지 않았으므로, 우선순위 큐에 넣지 않습니다.

• 3번 노드 : 현재 값(13)이 (8+10+2)보다 더 작으므로 갱신하지 않습니다.

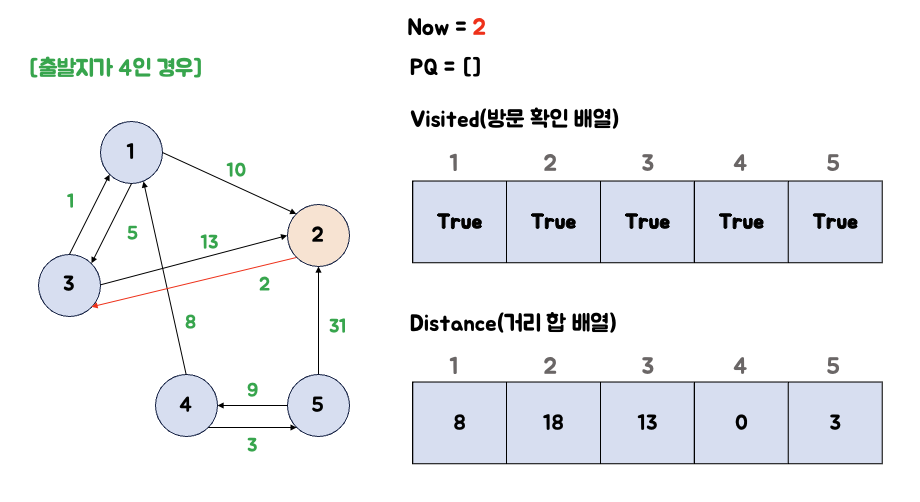
6. 큐에서 2번 노드를 꺼낸다.

큐에서 2를 꺼냅니다. 2번 노드는 이미 방문 처리가 되어 있으므로 동작하지 않습니다.

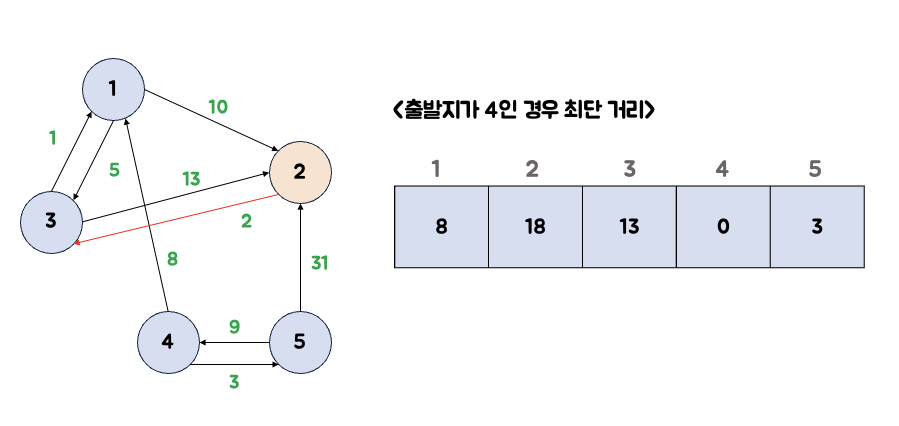
7. 결과

큐가 모두 비었으므로 동작을 멈춥니다.

코드로 구현하기 (Java)

import java.io.*;
import java.util.*;

public class Main {
    static List<Node>[] graph;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());
        int m = Integer.parseInt(br.readLine());
        
        graph = new ArrayList[n+1]; 
        for (int i = 0; i <= n; i++)  graph[i] = new ArrayList<>();

        StringTokenizer st;
        for(int i = 0 ; i < m; i++) {
            st = new StringTokenizer(br.readLine());
            int v = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());
            int cost = Integer.parseInt(st.nextToken());
            
            graph[v].add(new Node(w, cost));
        }

        int start = Integer.parseInt(br.readLine());

        dijkstra(n, start);
    }

    static void dijkstra(int n, int start) {
        boolean[] visited = new boolean[n+1];

        int[] distance = new int[n+1];
        Arrays.fill(distance, Integer.MAX_VALUE); // MAX 값으로 채워줍니다.
        distance[start] = 0; // 출발지는 거리가 0이므로 0으로 갱신해줍니다.

        PriorityQueue<Node> pq = new PriorityQueue<>();
        pq.offer(new Node(start, 0)); // 출발지를 큐에 넣습니다.

        while(!pq.isEmpty()) { // 큐가 빌 때까지 반복합니다.
            Node now = pq.poll();

            if(visited[now.index]) continue;
            visited[now.index] = true;

            for(Node next: graph[now.index]) {
                if(distance[next.index] > distance[now.index] + next.cost) { // 값을 비교하고 갱신합니다.
                    distance[next.index] = distance[now.index] + next.cost;
                    pq.offer(new Node(next.index, distance[next.index]));
                }
            }
        }

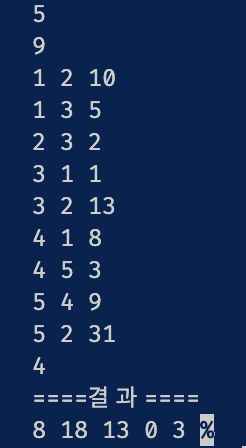
        System.out.println("====결과====");
        for(int i=1; i<n+1; i++) {
            if(distance[i] == Integer.MAX_VALUE) System.out.print(0+" ");
            else System.out.print(distance[i]+" ");
        }   
    }

    static class Node implements Comparable<Node> {
        int index;
        int cost;

        public Node(int index, int cost) {
            this.index = index;
            this.cost = cost;
        }

        @Override
        public int compareTo(Node n) {
            return Integer.compare(this.cost, n.cost);
        }
    }
}

입력은 예시의 그대로 입력해주었습니다.