에라토스테네스의 체

에라토스테네스의 체란?

에라토스테네스의 체란 소수를 찾는 방법입니다. 해당 방법은 마치 체로 치듯이 수를 걸러낸다고 해서 에라토스테네스의 체 라고 부른다고 합니다.

동작 방식

우리는 체에 집중해서 하나씩 소수가 아닌 수를 걸러낼 것 입니다.

즉, “소수를 찾고 해당 소수의 배수를 모두 지우면 소수만 남는다!” 입니다.

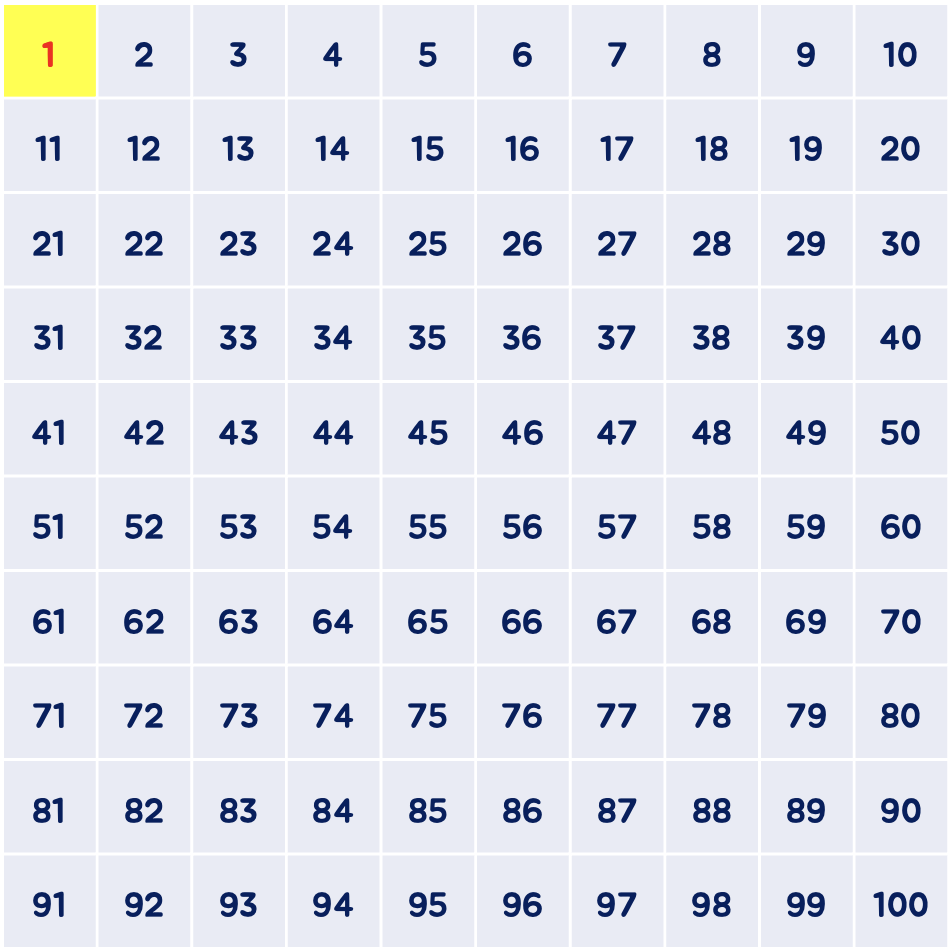
예를 들어, 100 이하의 자연수 중 소수를 모두 찾아보도록 하겠습니다.

(1) 1 제거

우선 소수도, 합성수도 아닌 유일한 자연수인 1을 제거합니다.

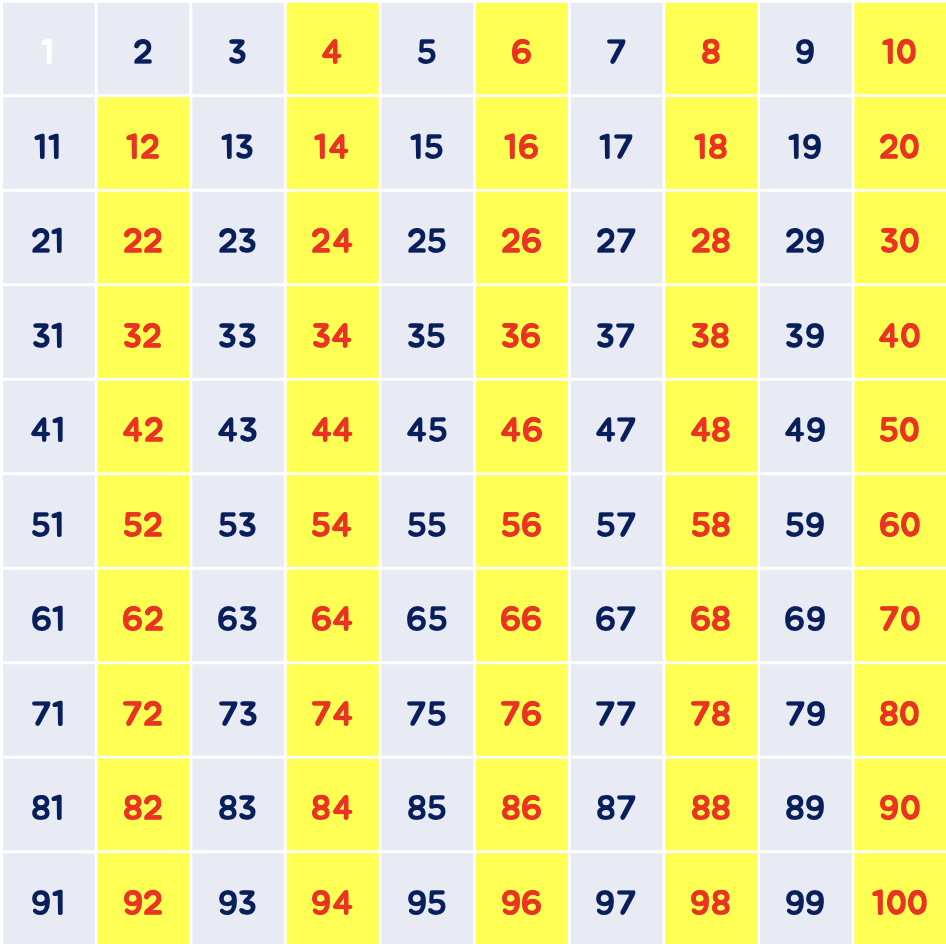
(2) 2를 제외한 2의 배수 제거

다음으로는 2를 제외한 2의 배수를 제거합니다. 무언가의 배수라는 것은 소수가 아니라는 것을 뜻하니까요!

(3) 3을 제외한 3의 배수 제거

다음은 3을 제외한 3의 배수를 제거합니다.

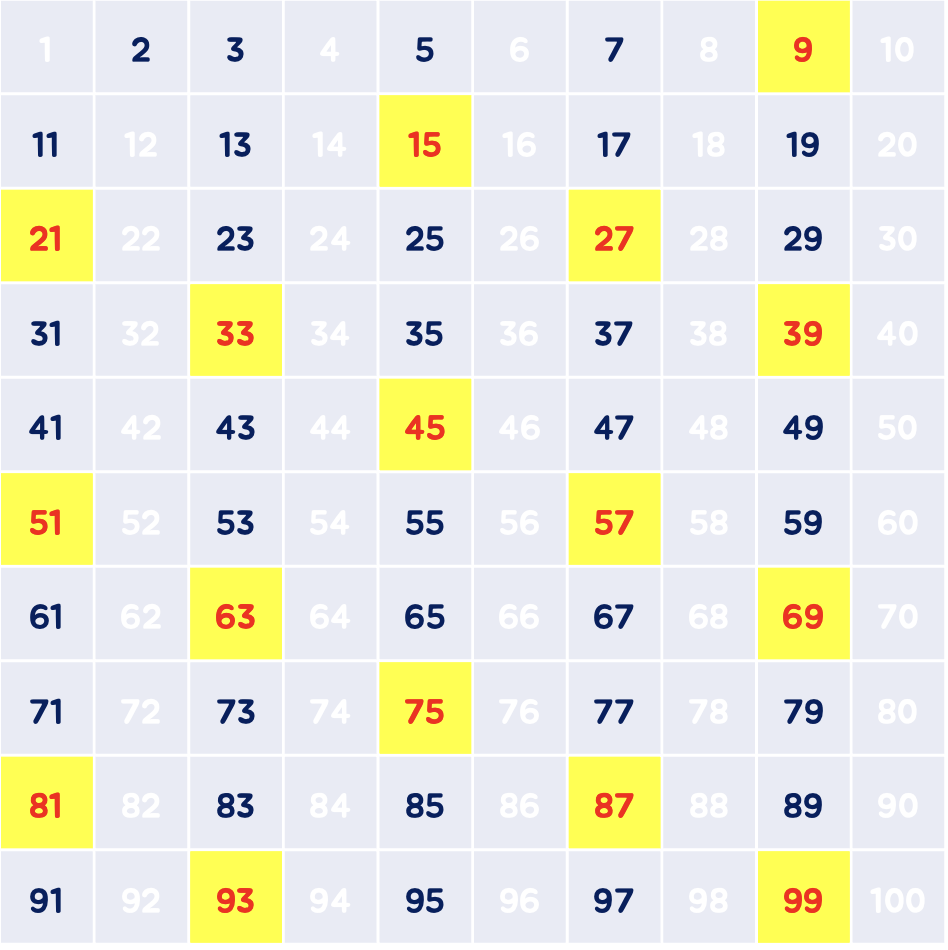
(4) 5를 제외한 5의 배수 제거

4는 2의 배수이므로 4의 배수는 이미 2의 배수를 제거할 때 제거되었습니다. 그러므로 4는 건너뛰고 5로 넘어갑니다!

(5) 7을 제외한 7의 배수 제거

7을 제외한 7의 배수를 제거합니다.

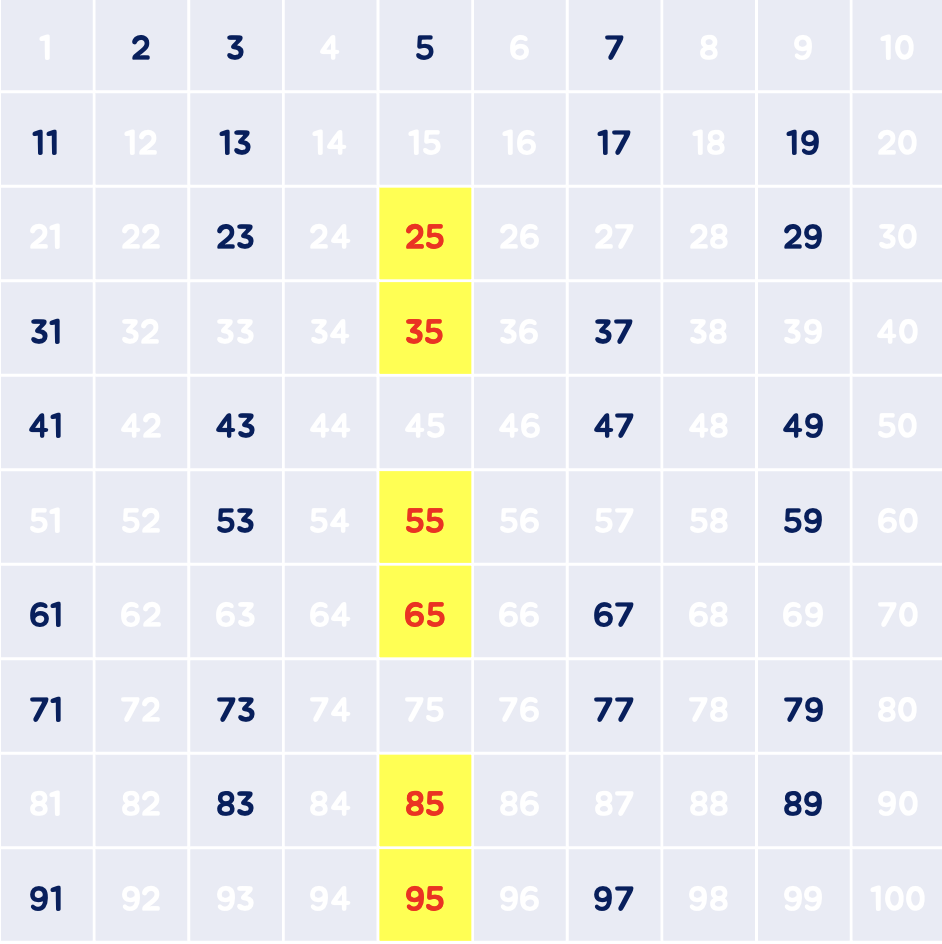
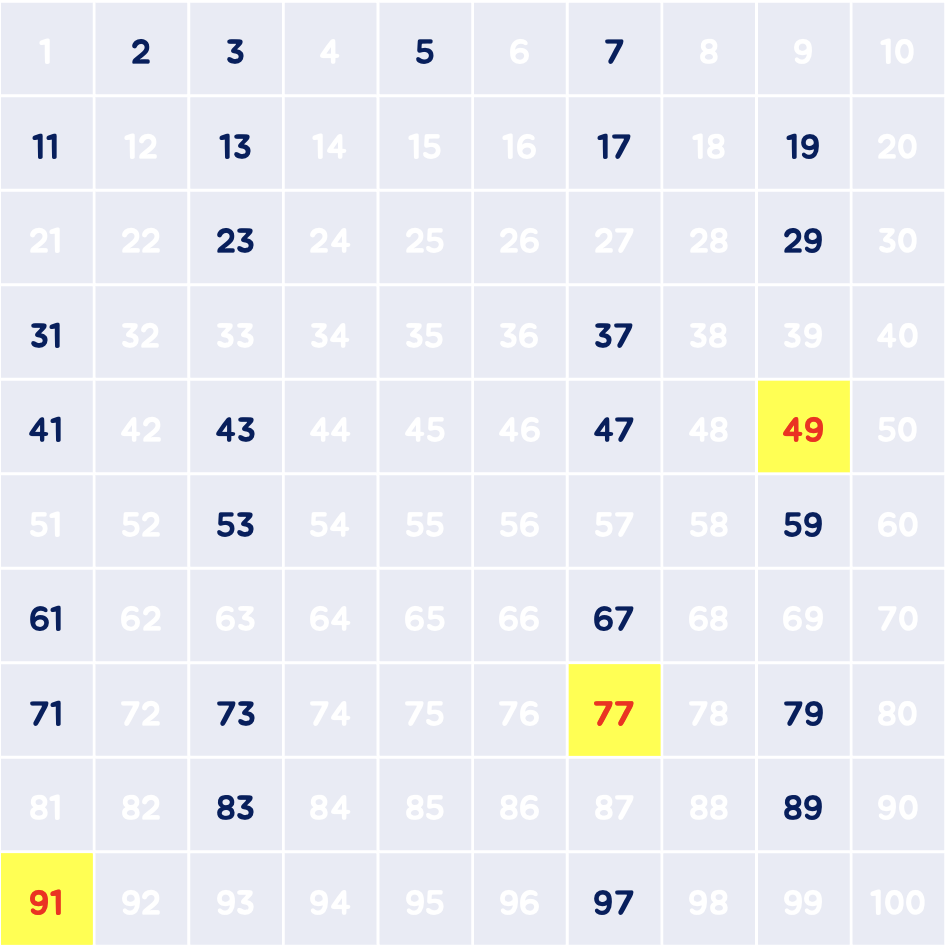
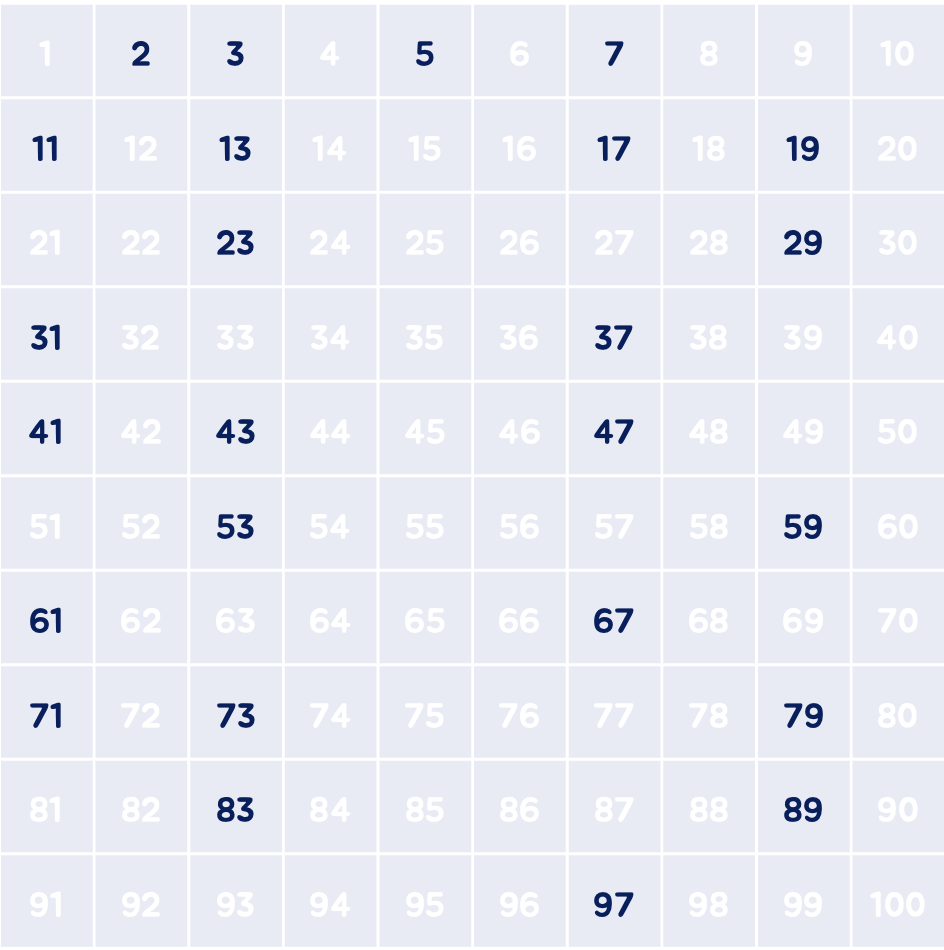
(6) 결과

아래 남은 숫자들은 소수입니다.

이렇게 소수를 찾고 배수를 모두 제거하는 것을 반복하면 이것이 바로 에라토스테네서의 체 동작 방식입니다!

그냥 보기에는 무식한 방식이라고 생각할 수 있지만, 숫자가 커질수록 제거하는 수가 줄어들기 때문에 빠르게 소수만을 찾을 수 있습니다.

에라토스테네스의 체 코드 (Java)

아래는 Java로 에라토스테네스의 체를 구현한 코드입니다.

public class Eratosthenes {
    private static void solution(int max_number) {
        boolean prime[] = new boolean[max_number+1];

        // 소수는 false
        // 소수가 아닌 수는 true
        prime[0] = prime[1] = true;

        for(int i=2; i*i<=max_number; i++) {
            if(!prime[i]) { // prime[i]가 소수라면
                for(int j=i*i; j<=max_number; j+=i) { // 소수의 배수는 소수가 아님
                    prime[j] = true;
                }
            }
        }

        for(int i=1; i<=max_number; i++) { // 소수 출력
            if(!prime[i]) System.out.println(i);
        }
    }
}

시간 복잡도는?

에라토스테네스의 체의 시간 복잡도는 O(Nlog(log N) 입니다!

소수 문제는 무조건 사용할 수 있을까?

그렇다면 에라토스테네스의 체를 모든 소수 문제에서 사용하는게 좋을까요? 당연히 답은 “NO” 입니다!

에라토스테네스의 체는 특정 범위 내의 소수를 판정하는 데에만 효율적이며, 주어진 단 하나의 숫자가 소수인지를 판별해야 하는 상황이라면 소수판정법 이라는 다른 방법을 사용하는 것이 더 효과적입니다.

참고
https://velog.io/@max9106/Algorithm-%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98-%EC%B2%B4
https://namu.wiki/w/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98%20%EC%B2%B4