카운팅 정렬(계수 정렬)

카운팅 정렬이란?

카운팅 정렬이란 단어 그대로 정렬 알고리즘 중 하나입니다. 그렇다면 앞에 붙은 카운팅은 무엇일까요? 무엇을 카운팅한다는 것일까요?

정답은 데이터의 값이 몇 번 등장했는지를 카운팅하는 것입니다.

대부분의 정렬은 데이터의 값을 직접 비교하여 정렬하는 경우가 많지만 데이터 값의 직접 비교는 시간 복잡도가 O(NlogN)보다 작아질 수 없다는 한계가 존재합니다.

그에 비해 카운팅 정렬은 O(N) 의 시간 복잡도를 자랑하는데요! 어떻게 가능한 것일까요?

동작 방식

아래 그림과 같은 배열을 정렬하고 싶다고 가정하고 동작 방식을 설명하겠습니다.

(1) 카운팅 배열 만들기

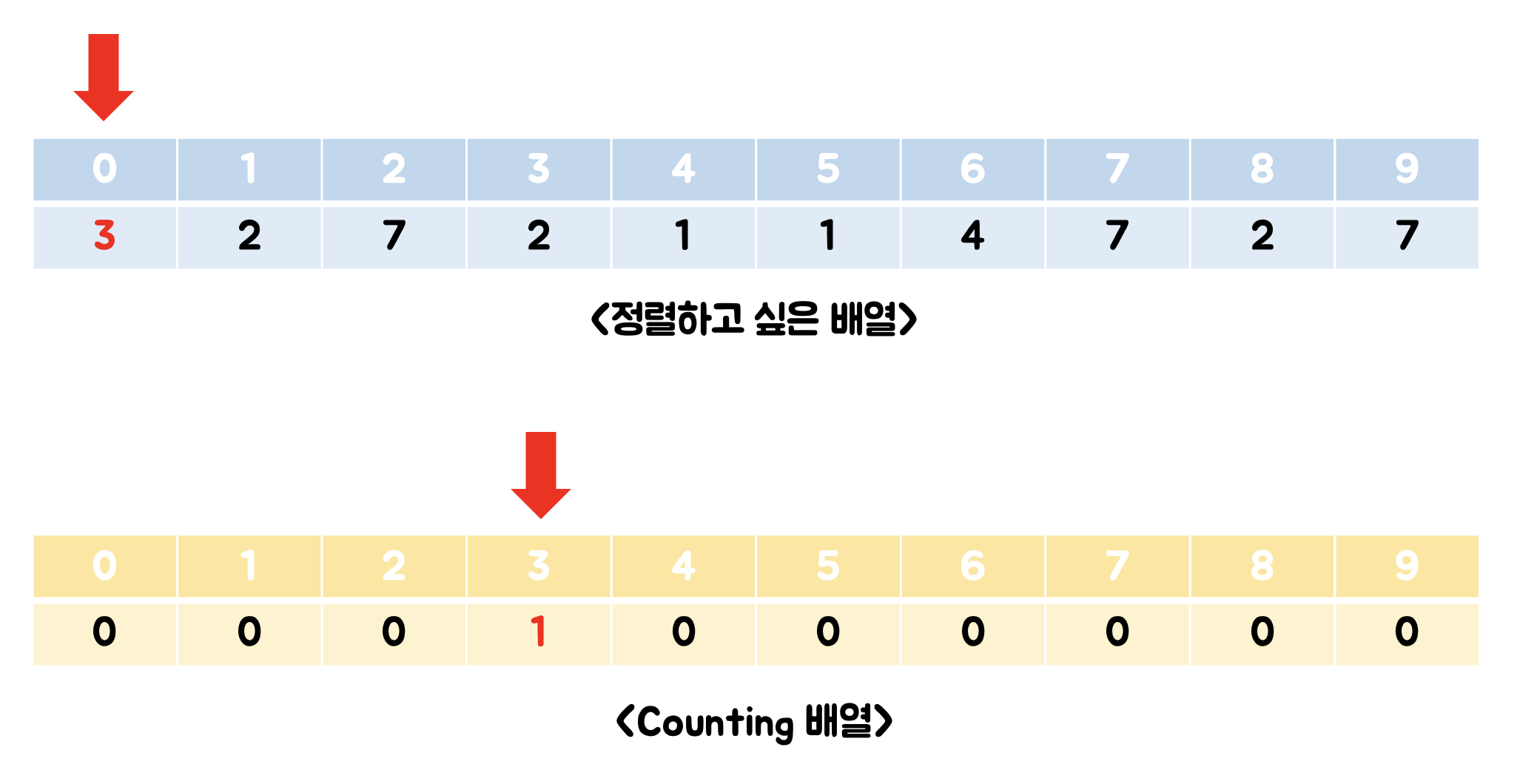
카운팅 정렬에는 기존 배열 외에도 카운팅 배열이 따로 필요합니다. 즉, 데이터가 얼마나 등장하는지를 배열 인덱스를 통해 기록하는 것입니다.

(1) 0번 인덱스의 데이터 값 카운팅하기

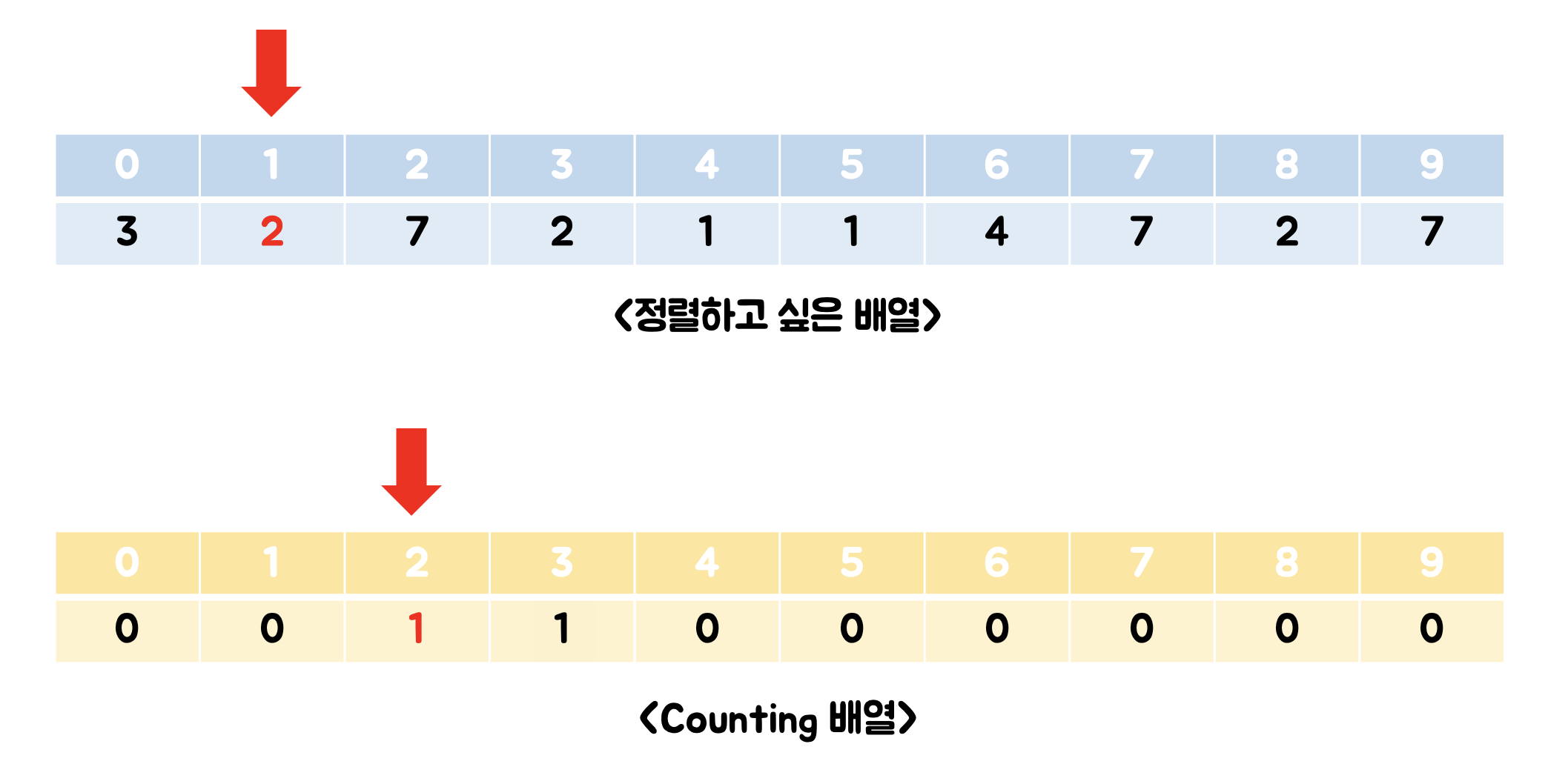
(2) 1번 인덱스의 데이터 값 카운팅하기

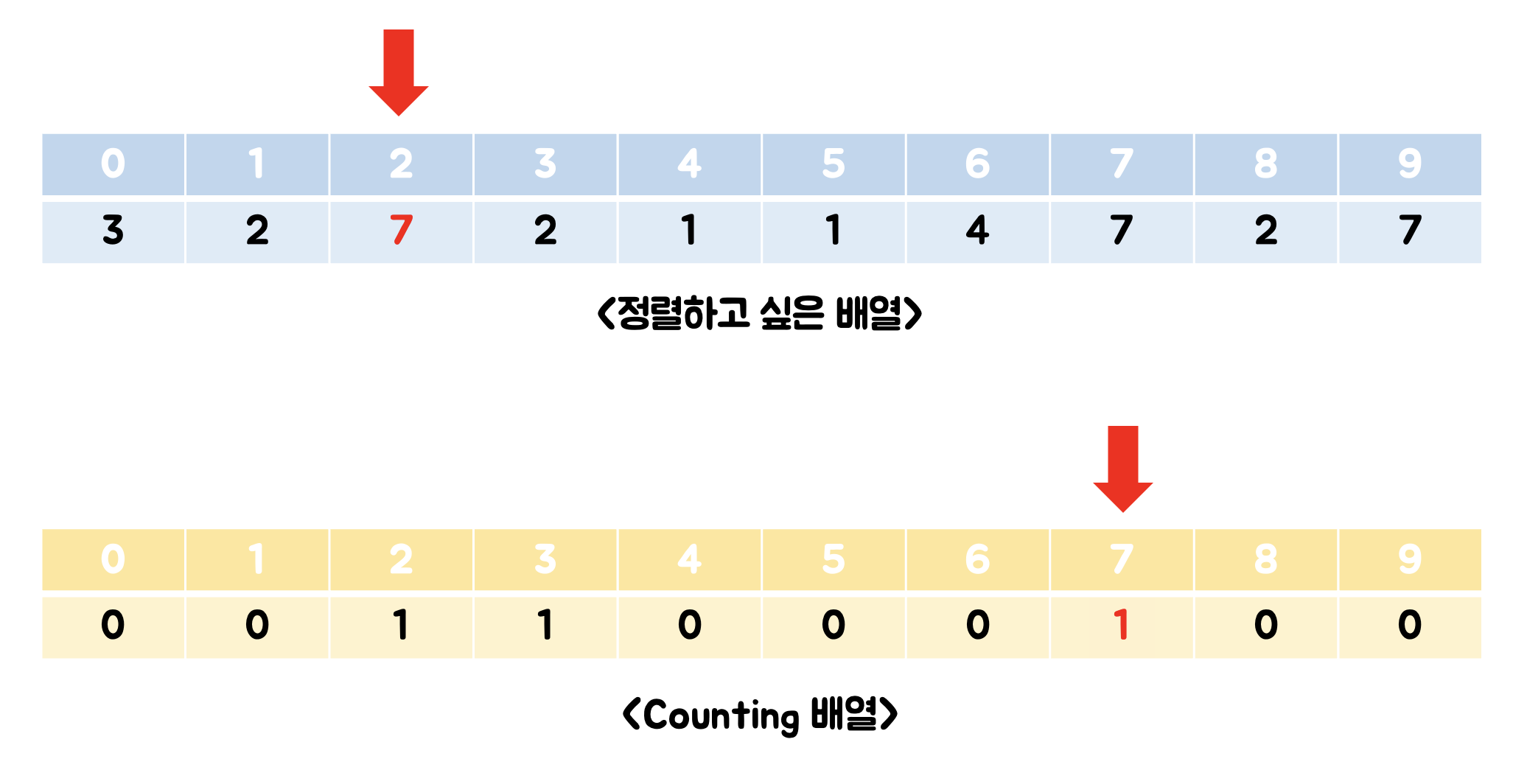
(3) 2번 인덱스의 데이터 값 카운팅하기

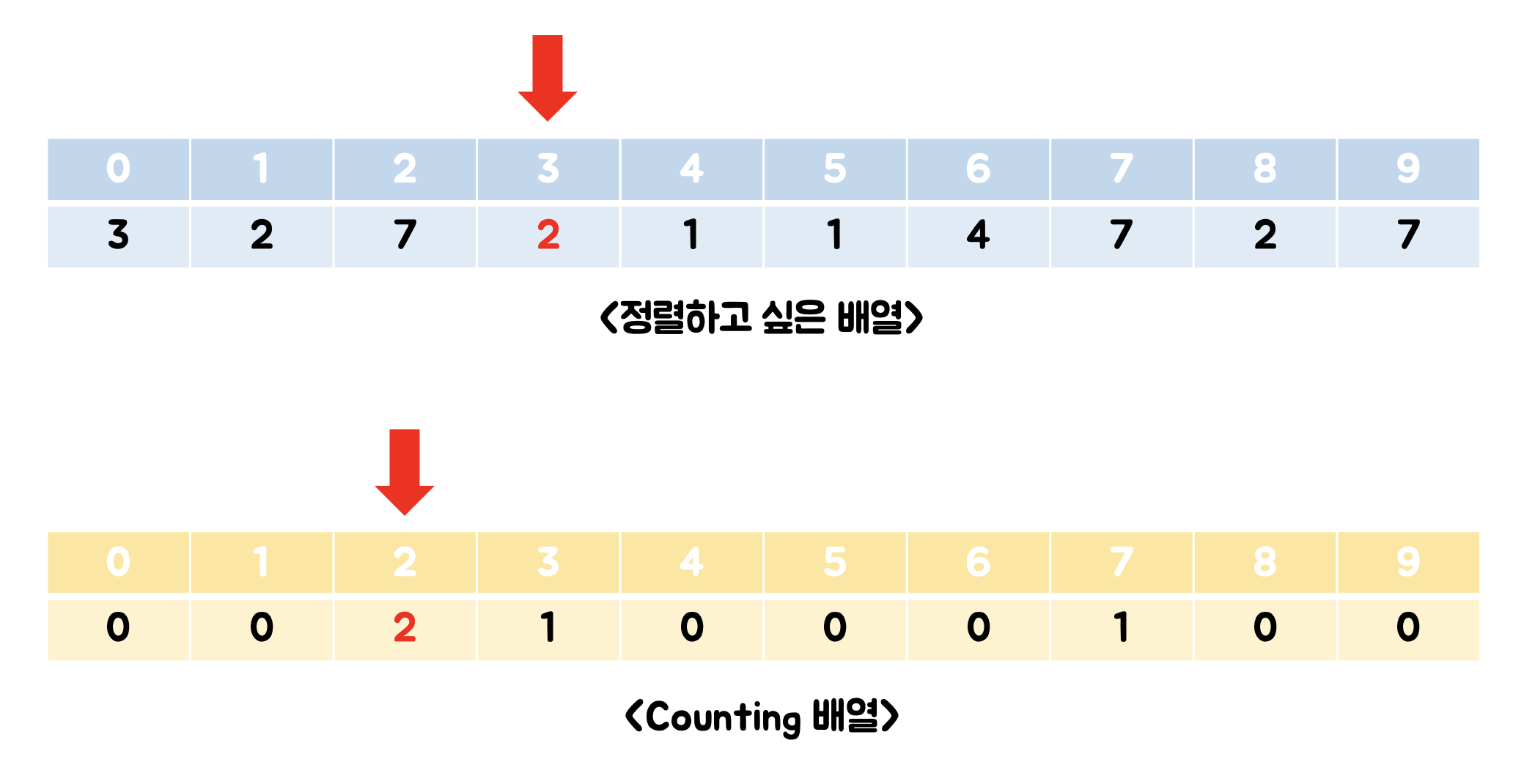
(4) 3번 인덱스의 데이터 값 카운팅하기

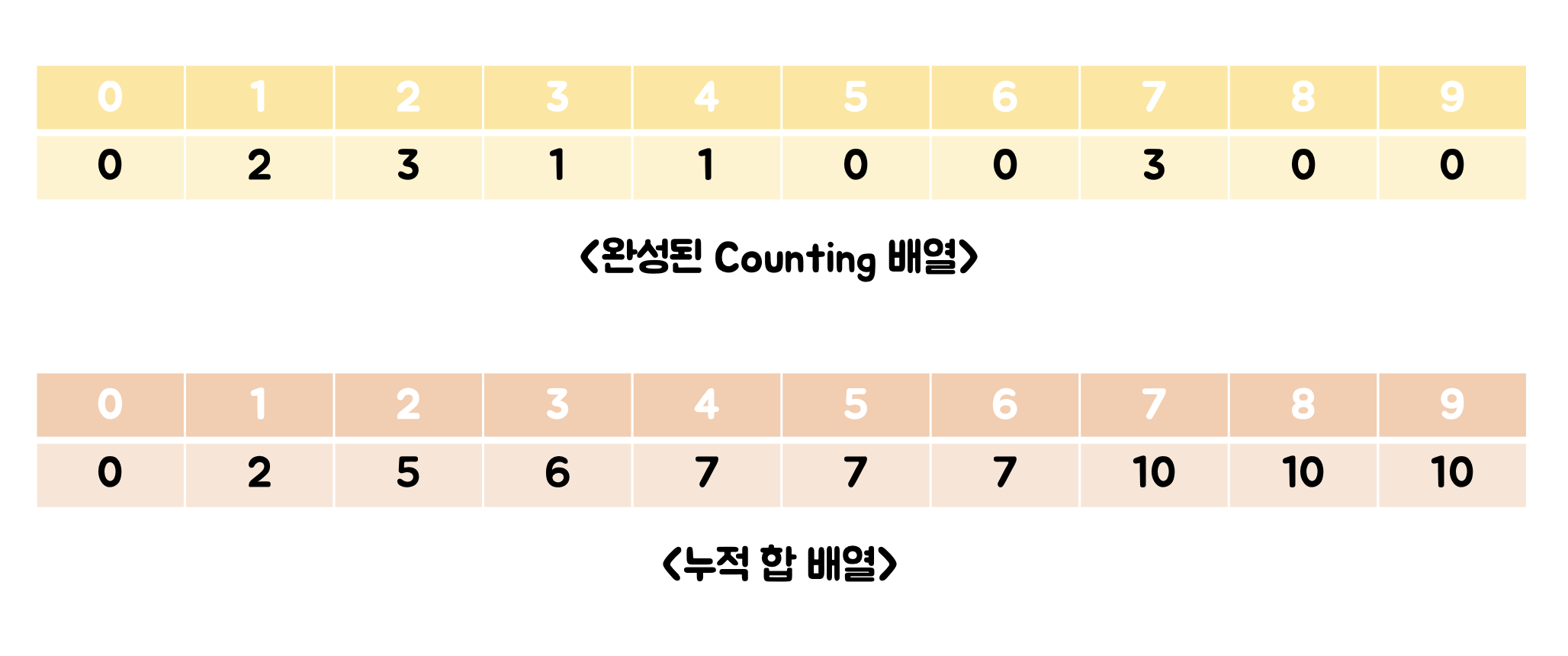
(5) 완성된 카운팅

이렇게 모든 배열의 값을 카운팅하면 아래와 같은 counting 배열이 만들어집니다.

(2) 누적 합 배열 만들기

카운팅 정렬을 위해서는 카운팅 배열의 누적 합 배열이 필요합니다.

arr[0] = arr[0]
arr[a+1] = arr[a] + arr[a+1]

의 수식을 통해 누적 합 배열을 손쉽게 구할 수 있습니다.

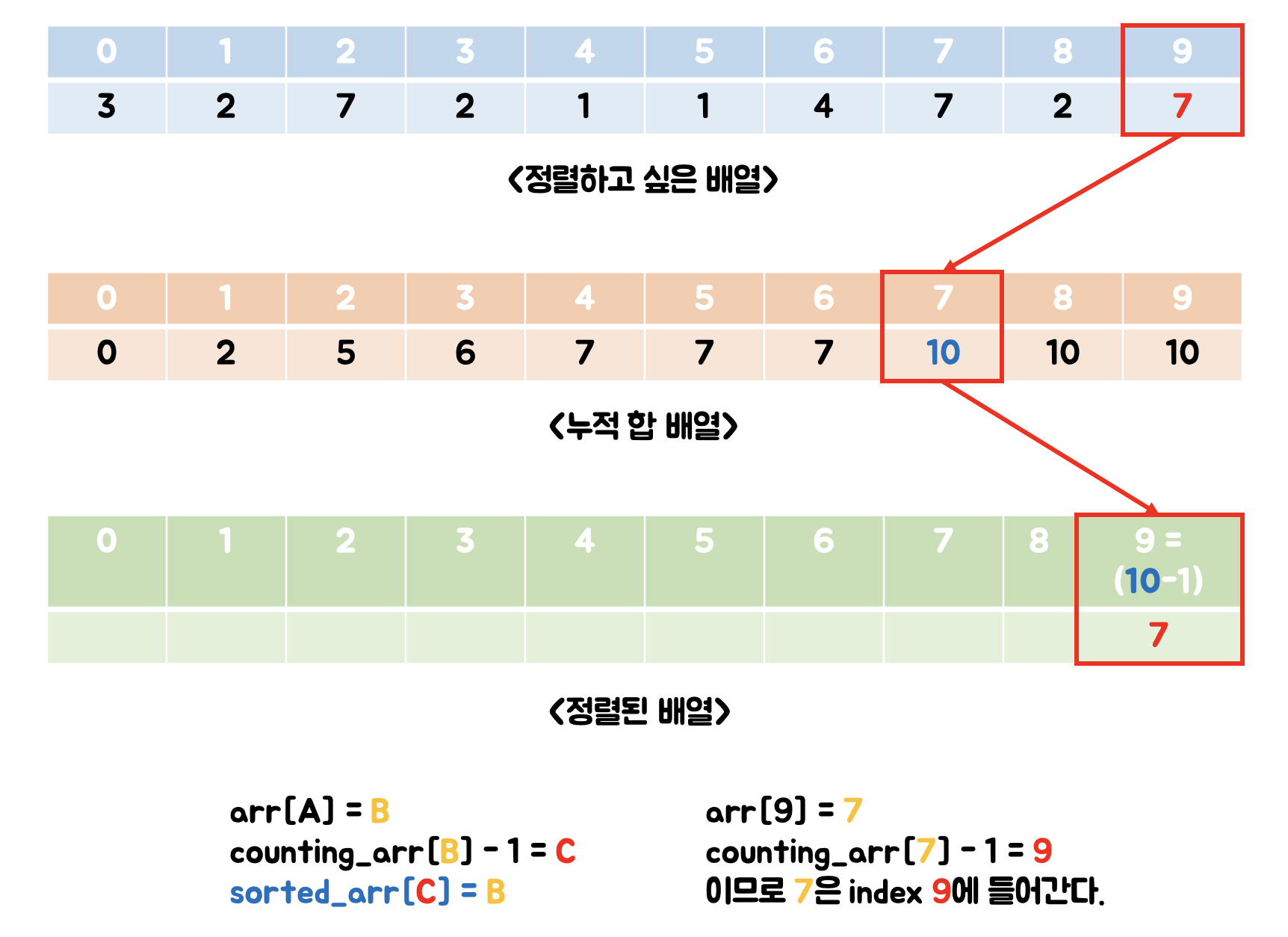
(3) 기존 배열과 누적 합 배열을 통해서 정렬된 배열 만들기

이제는 데이터의 자리를 정해주면 됩니다.

• 기존의 데이터의 값을
• 누적 합 배열의 인덱스로 가져가서
• 해당 인덱스에 있는 (값-1)을 해주면 정렬된 자리의 인덱스가 나옵니다.

말로만 보면 이해가 쉽지 않으니 그림을 함께 봅시다!

(1) 같은 숫자는 어떻게 들어가나요?

누적 합 배열의 값은 단순히 -1을 해서 가져가는 것이 아니라 값 자체가 1씩 줄어들어 다시 저장되는 것이므로 순서대로 잘 저장이 됩니다.

즉, 위의 그림에서 1이 빠진 뒤 누적 합 배열의 7번 인덱스는 9로 바뀌는 것이지요!!

(4) 결과

위 3번의 과정을 배열의 가장 뒷자리부터 반복한 결과는 아래 그림과 같습니다.

이와 같이

• 데이터의 개수를 표시하는 카운팅 배열을 만들고
• 카운팅 배열의 누적 합 배열을 구하고
• 누적 합 배열과 기존 배열을 통해 데이터의 자리를 결정하면 됩니다.

코드 (Java)

아래는 Java로 카운팅 정렬을 구현한 코드입니다.

public class Main {
    static int[] arr = new int[100]; // 기존 배열
    static int[] counting_arr = new int[31]; // 카운팅 배열
    static int[] sorted_arr =  new int[100]; // 정렬 결과를 담을 배열

    public static void main(String[] args) {
        for(int i=0; i<arr.length; i++) {
            // 0~30 사이의 랜덤한 값을 저장합니다.
            arr[i] = (int)(Math.random()*31);
        }

        // (1) 카운팅 배열 만들기
        for(int i=0; i<arr.length; i++) {
            counting_arr[arr[i]]++;
        }

        // (2) 누적 합 배열 만들기
        for(int i=1; i<counting_arr.length; i++) {
            counting_arr[i] += counting_arr[i-1];
        }

        // (3) 정렬된 배열 만들기
        for(int i=arr.length-1; i>=0; i--) {
            int number = arr[i];
            counting_arr[number]--;
            sorted_arr[counting_arr[number]] = number;
        }

        print(); // 비교 출력
    }

    private static void print() {
        System.out.println("<정렬 전>");
        for(int i=0; i<arr.length; i++) {
            if(i % 10 == 0) System.out.println();
			System.out.print(arr[i] + "\t");
        }

        System.out.println("<정렬 후>");
        for(int i=0; i<sorted_arr.length; i++) {
            if(i % 10 == 0) System.out.println();
			System.out.print(sorted_arr[i] + "\t");
        }
    }
}

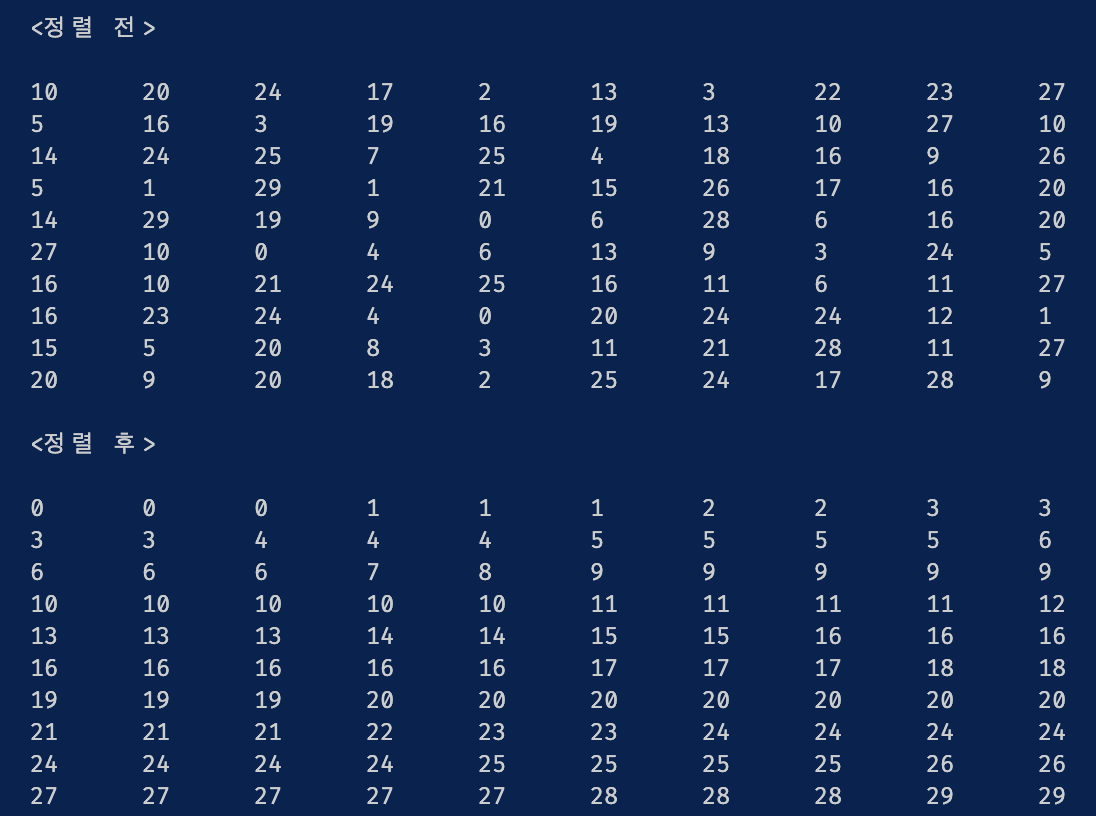
아래와 같이 잘 정렬된 것을 확인할 수 있습니다.

시간 복잡도는?

카운팅 정렬의 시간 복잡도는 앞서 언급한 것과 같이 O(N) 입니다! 엄청나죠..

정렬은 무조건 카운팅 정렬을 사용하는게 좋을까?

카운팅 정렬은 O(N)이라는 엄청 좋은 시간 복잡도를 가지고 있지만, 늘 좋은 것만은 아닙니다.

앞선 과정에서 봤듯이 정렬을 위해서는 추가적인 배열 선언이 필요하므로 메모리 소모가 발생하게 됩니다. 특히 정렬하고자 하는 데이터 값의 범위가 넓은 경우에는 퀵 정렬이나 병합 정렬 같은 다른 정렬 방식을 사용하는 것이 더 효과적일 수 있습니다.

참고
https://st-lab.tistory.com/104
https://8iggy.tistory.com/123